Koopman theory in Parameterization Method

引用于知乎Modern Koopman Theory For Dynamical Systems 笔记一 - 知乎 (zhihu.com)

Modern Koopman Theory For Dynamical Systems

最近一直在研究一个问题，参数化降阶方法中，对于一个给定的系统什么样的style得到的降阶模型更加准确，更加global？

这个问题准确说来自于文章^[1]提出的对于一些特殊系统的采用不同的style，而产生不同的结果的问题。本质上，不同的非线性系统适用于不同的style，而怎么去找到那个系统适合那个style？这是一个很大的困惑。其次，对于文章中提到的那几个非线性系统，他的特殊性，我没有一些很准确的认识。所以我希望能找一些别的理论来解释这个问题，从而找到这个问题的解。

为什么要学习koopman theory？对于上面提到的问题，一个很重要的点在于，对于一个系统，真正决定它的style选择的是线性部分还是非线性部分？实际上，在包括Haller等在内一系列人在处理近内共振时，采用的NFP-NR style的原因仅仅是因为线性部分的特征值的近内共振属性。有一个反例，在文章^[1]中被提到，对于一个线性部分存在近内共振的系统（i.e. 特征值的实部相当小）,研究发现NFP-NR并不是最优的方法，而是NFP-L，这和普遍的认识是相悖的。

那么我事实上推测，参数化的选择并不能仅仅由线性部分的特征值简单决定。似乎有一些概念类似于”非线性共振”是我需要找到的答案，即非线性项如何影响参数化。这类似于，对于强非线性系统和弱非线性系统的识别。对于问题再聚焦一点（如果我不能找到一个大而全的理论去解决参数化的选择），我们是否先简单的解决对于近内共振问题，多小的特征值实部算小？（这决定了参数化系数的分母的大小）

这些问题看是很让人浮想联翩，但又是无迹可寻的。好在有Koopman theory，这一研究如果将非线性系统线性化的理论，看能否找到一些能依靠的理论去解决这个问题。

The basic of koopman theory

Pro. Brunton 这篇review很经典，对于了解基本koopman theory的理论还是最前沿一些研究还是各个领域的应用都是很好的资料。这个章节以文中第二章为基础，简单介绍Koopman theory.

1.The definition of Koopman operator

考虑一个动力系统
$$
\frac{d}{dt}x(t)=f(x(t))
$$
这里$x\in\mathbb{R}^n$ 是状态空间中的变量，当然也有可能是在某些n维的流形上面，例如$x\in\mathcal{X}$.同时对于时间映射有$F^t:\mathcal{X}\rightarrow\mathcal{X}$,所以轨迹可以写成
$$
x(t)=F^t(x(0))
$$
这里定义观察函数(也别称为测量函数measurement function) $g:\mathcal{X}\rightarrow\mathbb{C}$, 表示从相空间到观测空间的映射，$\mathcal{G}(\mathcal{X})$表示观测函数的集合。在此基础上上面，我们可以定义Koopman算子$\mathcal{K}^t:\mathcal{G}(\mathcal{X})\rightarrow\mathcal{G}(\mathcal{X})$,满足以下等式的成立
$$
\mathcal{K}^tg(x)=g(F^t(x))
$$
这也可以被看作观测空间的时间映射
$$
g_t:=\mathcal{K}^tg,~g_0:=g
$$

2. Some properties in koopman theory

Koopman理论的最大特征就是可以把一个非线性的问题转换为一个无限维的线性问题，对于此$\mathcal{G}(\mathcal{X})$是一个线性的函数空间
$$
\mathcal{K}^t(\alpha_1g_1(x)+\alpha_2g_2(x))=\alpha_1g_1(F^t(x))+\alpha_2g_2(F^t(x))=\alpha_1\mathcal{K}^tg_1(x)+\alpha_2\mathcal{K}^tg_2(x)
$$
这允许了在函数空间$\mathcal{G}(\mathcal{X})$的线性化。

这里定义一个连续系统的无限小算子$\mathcal{L}$
$$
\mathcal{L}g:=\lim_{t\rightarrow0}\frac{\mathcal{K}^tg-g}{t}=\lim_{t\rightarrow0}\frac{g(F^t)-g}{t}
$$
这里的算子$\mathcal{L}$也被称作Lie 算子，他是关于g在向量场f(x)的Lie导数，那么对于$g(x)$的导数可以写作
$$
\frac{d}{dt}g(x(t))=\nabla g \cdot\dot{x}(t)=\nabla g\cdot f(x(t))
$$
同时其也等于Lie导数
$$
\frac{d}{dt}g(x(t))=\lim_{\tau\rightarrow0}\frac{g(x(t+\tau))-g(x(t))}{\tau}=\mathcal{L}g(x)
$$
等价于
$$
\mathcal{L}g=\nabla g\cdot f
$$
Lie算子满足一个连续时间的线性方程
$$
\frac{d}{dt}g=\mathcal{L}g
$$
对于一个很特殊的案例来说，将观测函数设为Identity function,$g(x)=x$.这对于上式的左边来说通常是$\dot{x}$，这和原来的状态方程一致。而对于等式的右端来说$\mathcal{L}x$，变成了函数空间$\mathcal{G}(\mathcal{X})$中大量(无限)的基的线性组合。这一个性质在后面一篇推导Koopman框架下的NNM和原本的理论之间关系的文章中有用到。

3. Eigenfunctions of Koopman operator

对于Koopman 算子的特征值和特征函数$\varphi(x)$，其满足以下等式
$$
\frac{d}{dt}\varphi(x)=\mathcal{L}\varphi(x)=\mu\varphi(x)
$$
这也代表Koopman 算子有
$$
\mathcal{K}^t\varphi=\lambda^t\varphi
$$
这其中隐含了Lie算子的特征值和Koopman算子的特征值之间的关系$\lambda^t=exp(\mu t)$,这也代表了这两个特征值之间的等价性

对于一个线性系统$\dot{x}=Ax$,对于其左特征向量$\xi^TA=\lambda\xi^T$,可以直接利用这个关系建造对应的Koopman特征函数
$$
\varphi(x):=\xi^Tx
$$

$$
\mathcal{K}\varphi(x)=\varphi(Ax)=\xi^TAx=\lambda\xi^Tx=\lambda\varphi(x)
$$

也就是说左特征向量给出了观测函数空间的时间不变的方向。

对于Koopman算子的特征函数，其具有两个任意的特征函数的乘积仍然是特征函数，例如
$$
\mathcal{K}(\varphi_1(x)\varphi_2(x))=\varphi_1(F(x))\varphi_2(F(x))=\lambda_1\lambda_2\varphi_1(x)\varphi_2(x)
$$
这条性质也可以用来建造无限特征函数空间。此外，类似于线性代数，观测函数空间的观测函数可以用特征函数的线性组合来表示，即$g\in span{\varphi_k}$
$$
g(x)=\sum_kv_k\varphi_k
$$

level-set of eigenfunction

对于特征函数的Level-set来说，代表了相空间中点集之间的关系。比如我们将特征函数写成极坐标的形式
$$
\varphi(x)=R(x)e^{i\Theta(x)},\lambda=re^{i\theta}
$$
定义子level-set为
$$
M_\varphi(C):={x\in\mathcal{X}:R(x)\leq C},A_\varphi:={x\in\mathcal{X}:\Theta(x)\leq \alpha}
$$
对于时间映射F有
$$
F(M_\phi(C))=M_\phi(rC),~F(A_\phi(\alpha))=A_\phi(\alpha+\theta)
$$
对于一个将左特征向量作为特征函数$\xi^Tx$的线性系统$\dot{x}=Ax$。我们可以看到特征函数将相空间分割为一个个level-set，代表着相空间中点的一个时间上的顺序

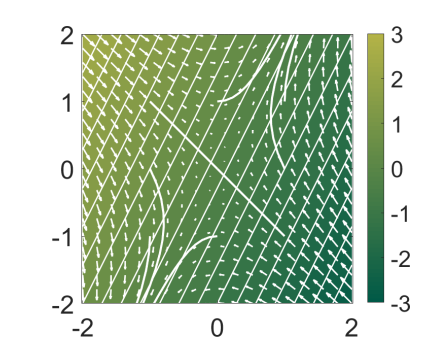
上图是针对一个特征值是实数的情况，如果特征值是复数，那么我们可以看到相空间中的levelset和lypunov函数一样，一圈一圈的围住不动点

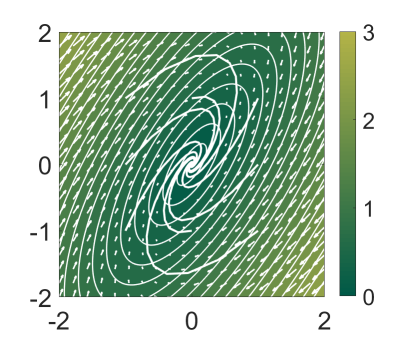
这类levelset也被称作isostables,这在后面的文献也会解释。

4. Koopman mode decomposition

对于一个向量的观测函数
$$
\begin{aligned}
g(x)=\left[
\begin{array}
{[c]}
g_{1} \\
g_{2} \\
\vdots&\\
g_{p}
\end{array}\right]
\end{aligned}
$$
对于每一个独立的观测函数，都可以用特征函数来线性表示
$$
\begin{aligned}
g(x)=\left[
\begin{array}
{[c]}
g_{1} \\
g_{2}\\
\vdots\\
g_{p}
\end{array}\right]
=\sum^{\infty}_{j=1}\varphi_j(x)v_j
\end{aligned}
$$
这里的$v_j$就代表了$j-th$ 的Koopman mode,其对应着特征函数$\varphi_j$.同时由于特征函数构建了连续系统的正交基，我可以通过正交来计算相应的mode
$$
\begin{aligned}
v_j=\left[
\begin{array}
{[c]}
<\varphi_j,g_{1}> \\
<\varphi_j,g_{2}>\\
\vdots\\
<\varphi_j,g_{p}>
\end{array}\right]
\end{aligned}
$$

5. A example of Koopman embedding

我们考虑一个动力系统
$$
\begin{align}
\dot{x}_1 &= \mu x_1 \
\dot{x}_2 &= \lambda(x_2-x^{2}_1)
\end{align}
$$
这里只需要将$x^2_1$设成一个观测函数，就可以很好的构成一个线性的三维Koopman空间
$$
\frac{d}{dt}\left[\begin{array}
{[c]}
y_1 \\
y_2 \\
y_3
\end{array}\right]=\begin{bmatrix}
\mu &0 &0\\
0 &\lambda &-\lambda \\
0 &0 &2\mu
\end{bmatrix}\left[\begin{array}
{[c]}
y_1 \\
y_2 \\
y_3
\end{array}\right]
$$
据此，我们可以求得这个线性算子的特征向量和特征值。根据理论求得线性系统的系数矩阵的左特征向量,再与变换后的坐标内积，即为Koopman算子的特征函数。观察矩阵，我们可以看出是一个分块对角矩阵，明显的得出一个特征值为$\mu$,另外一个特征值$\lambda$可以通过解另外一个对角块
$$
\left|\begin{bmatrix}
\lambda &-\lambda\\
0 &2\mu
\end{bmatrix}-kI\right|=0
$$
对于特征函数，将特征值代入等式，再求解线性方程，得到左特征向量(这和右特征值不一样)。再将其和$[y_1,y_2,y_3]^T$内积，可以得到特征函数
$$
\varphi_\mu=x_1,\varphi_\lambda=x_2-bx^2_1,b=\frac{\lambda}{\lambda-2\mu}
$$
可以通过这个例子验证前面的性质
$$
\frac{d}{dt}\varphi_\mu=\mu\varphi_\mu,\frac{d}{dt}\varphi_\lambda=\lambda\varphi_\lambda
$$

Some thinking for references

针对Koopman在动力系统里面的文献太过于繁杂了，对于其的应用逻辑还不是很了解。比如一些文献分析线性化，那么怎么线性化的最终目的是什么，产生的结果是什么，和NFP(Normal form方法)又有什么区别，这是一个很奇怪的东西。

1. A spectral characterization of nonlinear normal modes

这篇文献的主要目的是为了介绍从Koopman的框架怎么到非线性模态的内容。从这个角度来看，确实存在一些很隐晦的联系在现在的降阶方法和Koopman理论之间。在文章中，作者将非线性模态和Koopman算子的特征函数的零level-set联系到一起。说明实际上是可以从Koopman理论的框架转移到不变流形的求解上。

具体内容不赘述，但是值得一提的这里将Identity function的特征展开表达为
$$
id(x)=x=\sum_{(k_1,\dots,k_n)\in N^n}v_{k_1,\dots,k_n}\xi^{k_1}_1\dots\xi^{k_n}_n
$$
这里让$\xi_k=s_k(x)$,代表让特征函数代表一个新的坐标，表示最初的坐标和被特征函数定义的新的坐标系统之间的转换（这个意义和参数化中降阶的对应的概念还没有想好）。但是特征函数满足
$$
\dot{s_k}(x)=\lambda_k s_k(x),~\dot{\xi_k}=\lambda_k \xi_k
$$
这不就是和采用normal form style的方法不谋而合了吗？然而和文章中强调的可以跨越fold，这也印证了这个想法。如果是这样的，那么很失望，因为对我们最初的问题可能没有什么帮助。

1. Failing parametrizations: what can go wrong when approximating spectral submanifolds https://doi.org/10.1007/s11071-022-08154-3 ↩